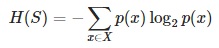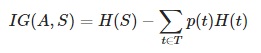ID3 is the first of a series of algorithms created by Ross Quinlan to generate decision trees.
Characteristics:
- ID3 does not guarantee an optimal solution; it can get stuck in local optimums
- It uses a greedy approach by selecting the best attribute to split the dataset on each iteration (one improvement that can be made on the algorithm can be to use backtracking during the search for the optimal decision tree)
- ID3 can overfit to the training data (to avoid overfitting, smaller decision trees should be preferred over larger ones)
- This algorithm usually produces small trees, but it does not always produce the smallest possible tree
- ID3 is harder to use on continuous data (if the values of any given attribute is continuous, then there are many more places to split the data on this attribute, and searching for the best value to split by can be time consuming).
Alternatives:
- ID3 is a precursor to both C4.5 algorithm, as well as C5.0 algorithm.
- C4.5 improvements over ID3:
- discrete and continuous attributes,
- missing attribute values,
- attributes with differing costs,
- pruning trees (replacing irrelevant branches with leaf nodes)
- C5.0 improvements over C4.5:
- several orders of magnitude faster,
- memory efficiency,
- smaller decision trees,
- boosting (more accuracy),
- ability to weight different attributes,
- winnowing (reducing noise)
- J48 is an open source Java implementation of the C4.5 algorithm in the Weka data mining tool
- C5.0 is being sold commercially (single-threaded version is distributed under the terms of the GNU General Public License) under following names: C5.0 (Unix/Linux), See5 (Windows)
Usage:
- The ID3 algorithm is used by training a dataset S to produce a decision tree which is stored in memory.
- At runtime, the decision tree is used to classify new unseen test cases by working down the tree nodes using the values of a given test case to arrive at a terminal node that tells you what class this test case belongs to.
Metrics:
- Entropy H(S) – measures the amount of uncertainty in the (data) set S
- Information gain IG(A) – measures how much uncertainty in S was reduced, after splitting the (data) set S on a attribute
- More details on both Entropy and Information Gain you’ll find here.
High-level inner workings:
- Calculate the entropy of every attribute using the data set S
- Split the set S into subsets using the attribute for which entropy is minimum (or, equivalently, information gain is maximum)
- Make a decision tree node containing that attribute
- Recurse on subsets using remaining attributes
Detailed algorithm steps:
- We begin with the original data set S as the root node
- In each iteration the algorithm iterates through every unused attribute of the data set S and calculates the entropy H(S) (or information gain IG(A)) of that attribute
- Next it selects the attribute which has the smallest entropy (or largest information gain) value
- The data set S is then split by the selected attribute (e.g. age < 50, 50 <= age < 100, age >= 100) to produce subsets of the data
- The algorithm continues to recurse on each subset, considering only attributes never selected before
- Recursion on a subset may stop in one of these cases:
- every element in the subset belongs to the same class (+ or -), then the node is turned into a leaf and labelled with the class of the examples
- there are no more attributes to be selected, but the examples still do not belong to the same class (some are + and some are -), then the node is turned into a leaf and labelled with the most common class of the examples in the subset
- there are no examples in the subset, this happens when no example in the parent set was found to be matching a specific value of the selected attribute, for example if there was no example with age >= 100. Then a leaf is created, and labelled with the most common class of the examples in the parent set
- Throughout the algorithm, the decision tree is constructed with each non-terminal node representing the selected attribute on which the data was split, and terminal nodes representing the class label of the final subset of this branch
Python implementation:
- Create a new python file called id3_example.py
- Import logarithmic capabilities from math lib as well as the operator library
from math import log import operator - Add a function to calculate the entropy of a data set
def entropy(data): entries = len(data) labels = {} for feat in data: label = feat[-1] if label not in labels.keys(): labels[label] = 0 labels[label] += 1 entropy = 0.0 for key in labels: probability = float(labels[key])/entries entropy -= probability * log(probability,2) return entropy - Add a function to split the data set on a given feature
def split(data, axis, val): newData = [] for feat in data: if feat[axis] == val: reducedFeat = feat[:axis] reducedFeat.extend(feat[axis+1:]) newData.append(reducedFeat) return newData - Add a function to choose the best feature to split on
def choose(data): features = len(data[0]) - 1 baseEntropy = entropy(data) bestInfoGain = 0.0; bestFeat = -1 for i in range(features): featList = [ex[i] for ex in data] uniqueVals = set(featList) newEntropy = 0.0 for value in uniqueVals: newData = split(data, i, value) probability = len(newData)/float(len(data)) newEntropy += probability * entropy(newData) infoGain = baseEntropy - newEntropy if (infoGain > bestInfoGain): bestInfoGain = infoGain bestFeat = i return bestFeat - According to step 6 of the “Detailed algorithm steps” section above, there are certain cases in which the recursion may stop. If we don’t meet any of the stopping conditions, then the small function below will allow us to choose the best feature depending on the “majority”:
def majority(classList): classCount={} for vote in classList: if vote not in classCount.keys(): classCount[vote] = 0 classCount[vote] += 1 sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True) return sortedClassCount[0][0] - Finally add the main function to generate the decision tree
def tree(data,labels): classList = [ex[-1] for ex in data] if classList.count(classList[0]) == len(classList): return classList[0] if len(data[0]) == 1: return majority(classList) bestFeat = choose(data) bestFeatLabel = labels[bestFeat] theTree = {bestFeatLabel:{}} del(labels[bestFeat]) featValues = [ex[bestFeat] for ex in data] uniqueVals = set(featValues) for value in uniqueVals: subLabels = labels[:] theTree[bestFeatLabel][value] = tree(split\(data, bestFeat, value),subLabels) return theTree
Voilà
Resources:
- Ross Quinlan’s Homepage (http://www.rulequest.com/Personal)
- Ross Quinlan on Wikipedia (http://en.wikipedia.org/wiki/Ross_Quinlan)
- ID3 algorithm description on Wikipedia (http://en.wikipedia.org/wiki/ID3_algorithm)
- C4.5 algorithm description on Wikipedia (http://en.wikipedia.org/wiki/C4.5_algorithm)
- Measuring Entropy (data disorder) and Information Gain (https://mariuszprzydatek.com/2014/10/31/measuring-entropy-data-disorder-and-information-gain)